Beneficiation experiment- Ore size analysis

Size of the particle is an important consideration in Mineral Beneficiation because of the following main reasons:

---Energy consumed for reducing the size of the particles depends on size.

---Size of the particles determines the type of size reduction equipment, beneficiation equipment and other equipment to be employed. The size of the particle of standard configuration like sphere and cube can easily be specified. For example, the size of a spherical particle is its diameter (d) and that of a cubical particle is the length of its side (l) as shown in Figure 1.

Figure 1 Spherical and cubical particles.

As the mineral particles are irregular in shape, it is difficult to define and determine their size. The size of a particle is defined by comparison with a standard configuration, normally a spherical particle.

Equivalent size or equivalent diameter of an irregular particle is defined as the diameter of a spherical particle which behaves similar to an irregular particle under specified conditions.

Surface diameter is defined as a diameter of a spherical particle having the same surface area as the irregular particle.

Volume diameter is defined as the diameter of a spherical particle having the same volume as the irregular particle.

In mineral industry, the side of a square aperture through which a particle just passes is taken as the size of the particle even though little or no importance is given to its shape. Standard Test Sieves are used in the mineral industry to measure the size of the small and the fine particles, usually down to 74 microns.Test Sieve is a circular shell of brass having an 8 inch diameter and being about 2 inch high as shown in Figure 2.

Figure2 Test sieve

Sieve cloth is made of wire, woven to produce nominally uniform cloth apertures (openings). The sieve cloth is placed in the bottom of the shell so that material can be held on the sieve.

Aperture (or Opening) is a distance between two parallel wires.

Mesh number is the number of apertures per linear inch. Sieves are designated by mesh number.

Mesh size is the size of an aperture i.e. the distance between two parallel wires. As mesh number increases, mesh size decreases.

Sieve Scale is the list of successive sieve sizes used in any laboratory, taken in order from coarsest to finest.

Standard Sieve Scale is the sieve scale adopted for size analyses and general testing work to facilitate the interchangeability of results and data. In this standard sieve scale, the sizes of successive sieves in series form a geometric progression.

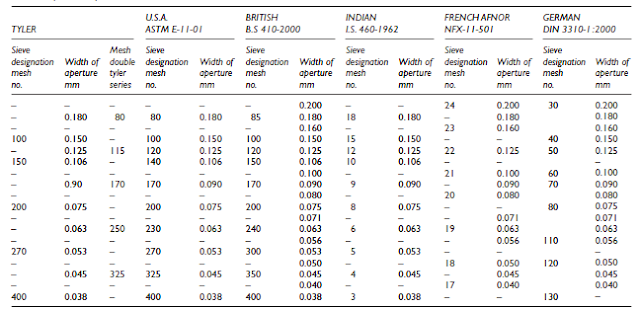
 For a standard sieve scale, the reference point is 74 microns, which is the aperture of a 200 mesh woven wire sieve. There are different standards of test sieves shown as table 1.

Table 1-1 Comparison of test sieves of different standards.

Table 1-2 Comparison of test sieves of different standards.

For most size analyses it is usually impracticable and unnecessary to use allthe sieves in a particular series. For most purposes, alternative sieves are quite adequate.For accurate work over certain size ranges of particular interest, consecutive sieves may be used. Intermediate sieves should never be chosen at random, as the data obtained will be difficult to interpret. In general, the sieve range should be chosen so that no more than about 5% of the sample material it retained on the coarsest sieve, or passes the finest sieve. These limits may be lowered for more accurate work

1 SIEVE ANALYSIS

It is a method of size analysis. It is performed to determine the percentage weight of closely sized fraction by allowing the sample of material to pass through a series of test sieves.

Closely sized material is the material in which the difference between maximum and minimum sizes is less. Sieving can be done by hand or by machine. The hand sieving method is considered more effective as it allows the particles to present in all possible orientations on to the sieve surface. However, machine sieving is preferred for routine analysis as hand sieving is long and tedious. Table model sieve shaker and Ro-tap sieve shaker (Figures 3 and 4) are the two principal machines used in a laboratory for sieve analysis. Owing to irregular shapes, particles cannot pass through the sieve unless they are presented in a favourable orientation, particularly with the fine particles. Hence there is no end point for sieving. For all practical purposes, the end point is considered to have been reached when there is little amount of material passing through after a certain length of sieving. Sieving is generally done dry. Wet sieving is used when the material is in the form of slurry. When little moisture is present, a combination of wet and dry sieving is performed by initially adding water.

Figure 3 Table model sieve shaker.

Figure 4 Ro-tap sieve shaker.

2 TESTING METHOD

The sieves chosen for the test are arranged in a stack, or nest, starting from the coarsest sieve at the top and the finest at the bottom. A pan or receiver is placed below the bottom sieve to receive the final undersize, and a lid is placed on top of the coarsest sieve to prevent escape of the sample.

Figure 5 Sieve analysis at the end of sieving.

The material to be tested is placed on the uppermost coarsest sieve and closed with lid. The nest is then placed in a Sieve Shaker and sieved for certain time. Figure 5 shows the sieve analysis at the end of the sieving. The material collected on each sieve is removed and weighed. The complete set of values is known as Particle Size Distribution data. Particle size distribution refers to the manner in which particles are quantitatively distributed among various sizes;in other words a statistical relation between quantity and size. Particle size distribution

data is presented in a tabular form as shown in Table 2.The weight percentages of the material retained on each sieve are to be calculated to form differential analysis. Cumulative weight percentage retained is obtained from differential analysis by adding, cumulatively, the individual differential weight percentages from the top of the table. Cumulative weight percentage passing is obtained by adding, cumulatively, the individual weight percentages from the bottom of the table.

All the fractions are fairly closely sized (except first fraction). Hence the size of the particles in each fraction may be calculated as arithmetic mean of the limiting sizes.

Table 2 Particle size distribution data from size analysis test

3.PRESENTATION OF PARTICLE SIZE DISTRIBUTION DATA

Particle size distribution data is best presented for use in the form of graphs (Figure 6). The simplest method is to plot a histogram of the weight percent of the material in the size interval against the size interval. When the size intervals are small enough, the histogram can be presented as a continuous curve taking the middle points of the histogram. In other words, a graph is plotted between the weight percent of the material as ordinate and the arithmetic mean size as abscissa. It is called a linear scale frequency plot. It gives the quantitative picture of the relative distribution of the material over the entire size range. In many cases, the data is more commonly plotted as cumulative weight percent passing versus actual size of opening. It is called a linear scale cumulative plot.

Figure 6 Graphical presentation of particle size distribution data.

The same graphs can also be drawn on semi-logarithmic graph paper for satisfactory spreading of the data on fine size region. 80% passing size (D80) is the size of the sieve at which 80% of the particles pass through that sieve. 80% passing size can be determined from the plot of cumulative weight percent passing versus sieve size as shown in Figure 7. F80 is the 80% passing size of the feed material. P80 is the 80% passing size of the product material. 80% passing size is used in all calculations to determine energy requirements for reducing the size of the particles by comminution equipment.

Figure 7 Plot for determination of 80% passing size D80.

4.APPLICATIONS OF PARTICLE SIZE DISTRIBUTION DATA

1 Comparative efficiencies of comminution units by relating the work done and the product sizes can be studied.

2 Particle surface areas can be calculated from size analysis.

3 Power required to crush and/or grind an ore from a given feed size to a given product size can be estimated from size analyses of the feed and the products.

4 The calculation of the sizing efficiency of a classifier or cyclone can be closely estimated from size analyses of the feed and the products.

5 SUB-SIEVE SIZING

Sizing of the particles having size less than 40 microns is known as Sub-sieve sizing.

The particles at fine sizes are termed as slimes and d colloids. The table 3 are the approximate size ranges of different particles

Table 3 Approximate size ranges of different particles

Size analysis methods used for the particles less than 40 microns are shown in Table 4.

Table 4 Size analysis methods for sub-sieve sizing.

Sedimentation and elutriation techniques are based on the settling behaviour of the particles of various sizes and the analysis is made by separating the particles into various size fractions. Microscopic sizing is similar to measurement with a yardstick. The particles are sprinkled on a glass slide or mounted in some way on a slide and the size of individual particles is measured under the microscope. Laser beam particle size analysis is of recent origin. The PSM system has been installed in several Mineral Beneficiation plants for continuous measurement of particle size.

In industry, classifiers and hydrocyclones are used for sizing sub-sieve size particles. Fine particles are more difficult to handle and beneficiate. Greater stress is to be given on the process of fine particles not only to recover the values but also to control pollution.

sinonine can also provide sand washing plant epc.